8.6 空间直线、平面的垂直
2024-07-18 22:06:14 新建
与平行关系类似,垂直也是空间直线、平面之间的一种特殊位置关系, 它在研究空间图形问题中具有重要的作用.类比平行关系的研究过程, 本节将研究空间直线、平面之间的垂直关系, 重点研究这些垂直关系的判定和性质.
8.6.1 直线与直线垂直
空间两条直线的位置关系有三种: 平行直线、相交直线和异面直线. 在初中我们已经研究了平行直线和相交直线. 本节我们主要研究异面直线, 首先研究如何刻画两条异面直线的位置关系.
观察
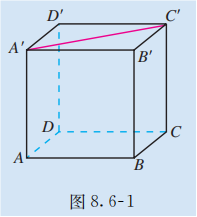
如图 8.6-1, 在正方体 中, 直线 与直线 , 直线 与直线 都是异面直线, 直线 与 相对于直线 的位置相同吗? 如果不同, 如何表示这种差异呢?
思路
研究异面直线所成的角, 就是通过平移把异面直线转化为相交直线. 这是研究空间图形的一种基本思路,即把空间图形问题转化为平面图形问题.
我们知道, 平面内两条直线相交形成 4 个角, 其中不大于 的角称为这两条直线所成的角(或夹角), 它刻画了一条直线相对于另一条直线倾斜的程度. 类似地,我们也可以用 “异面直线所成的角” 来刻画两条异面直线的位置关系.
定义
如图 8.6-2, 已知两条异面直线 , 经过空间任一点 分别作直线 , 我们把直线 与 所成的角叫做异面直线 与 所成的角 (或夹角).
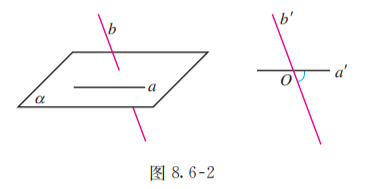
如果两条异面直线所成的角是直角, 那么我们就说这两条异面直线互相垂直. 直线 与直线 垂直, 记作 .
当两条直线 相互平行时, 我们规定它们所成的角为 . 所以空间两条直线所成角 的取值范围是 .
思考
直线 所成角的大小与点 的位置有关吗?
例 1
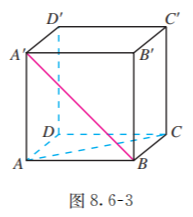
如图 8.6-3, 已知正方体 .
(1) 哪些棱所在的直线与直线 垂直?
(2) 求直线 与 所成的角的大小.
(3) 求直线 与 所成的角的大小.
解:
(1) 棱 所在直线分别与直线 垂直.
(2) 因为 是正方体, 所以 , 因此 为直线 与 所成的角. 又因为 , 所以直线 与 所成的角等于 .
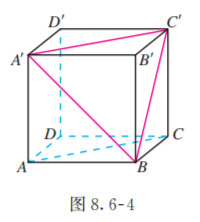
(3) 如图 8.6-4, 连接 . 因为 是正方体, 所以 平行且相等于 . 从而四边形 是平行四边形, 所以 . 于是 为异面直线 与 所成的角.
连接 , 易知 是等边三角形, 所以 .从而异面直线 与 所成的角等于 .
例 2
如图 8.6-5 (1), 在正方体 中, 为底面 的中心. 求证 .
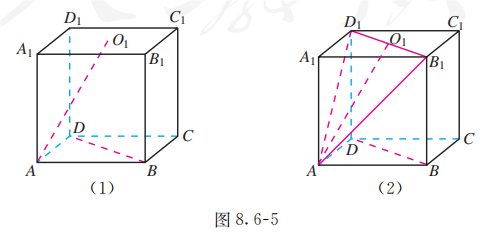
分析:
要证明 , 应先构造直线 与 所成的角, 若能证明这个角是直角, 即得 .
证明:
如图 8.6-5 (2), 连接 .
是正方体,
平行且相等于 .
四边形 是平行四边形.
.
直线 与 所成的角即为直线 与 所成的角.
连接 , 易证 .
又 为底面 的中心,
为 的中点,
.
.
从例 1 与例 2 的解答可以看到, 为了简便, 求异面直线 所成的角时, 点 常取在两条异面直线中的一条上. 例如取在直线 上, 然后经过点 作直线 , 那么 与 所成的角就是异面直线 与 所成的角(图 8.6-6).

练习
1.
判断下列命题是否正确, 正确的在括号内画 “ ”, 错误的画 “ ”.
(1) 如果两条平行直线中的一条与已知直线垂直, 那么另一条也与已知直线垂直.
(2) 垂直于同一条直线的两条直线平行.
2.
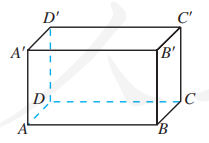
如图, 在长方体 的各条棱所在直线中,
(1) 与直线 垂直的直线有 条;
(2) 与直线 异面且垂直的直线有 条;
(3) 与直线 和 都垂直的直线有 条;
(4) 与直线 和 都垂直且相交的直线是直线 .
3.
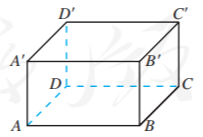
如图, 在长方体 中, , 求:
(1) 直线 和 所成的角的大小;
(2) 直线 和 所成的角的大小.
4.
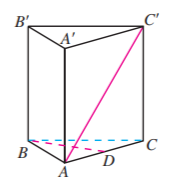
如图, 在正三棱柱 中, 为棱 的中点, , 求证 .
8.6.2 直线与平面垂直
在日常生活中, 我们对直线与平面垂直有很多感性认识. 比如, 旗杆与地面的位置关系(图 8.6-7), 教室里相邻墙面的交线与地面的位置关系等, 都给我们以直线与平面垂直的形象.

观察
如图 8.6-8, 在阳光下观察直立于地面的旗杆 及它在地面的影子 . 随着时间的变化, 影子 的位置在不断地变化, 旗杆所在直线 与其影子 所在直线是否保持垂直?
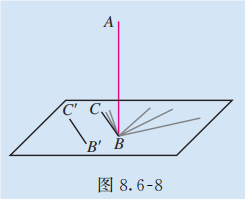
答
事实上, 随着时间的变化, 尽管影子 的位置在不断地变化, 但是旗杆 所在直线始终与影子 所在直线垂直. 也就是说, 旗杆 所在直线与地面上任意一条过点 的直线垂直.对于地面上不过点 的任意一条直线 , 总能在地面上找到过点 的一条直线与之平行, 根据异面直线垂直的定义, 可知旗杆 所在直线与直线 也垂直. 因此, 旗杆 所在直线与地面上任意一条直线都垂直.
定义
一般地, 如果直线 与平面 内的任意一条直线都垂直, 我们就说直线 与平面 互相垂直, 记作 . 直线 叫做平面 的垂线, 平面 叫做直线 的垂面. 直线与平面垂直时, 它们唯一的公共点 叫做垂足.
画直线与平面垂直时, 通常把直线画成与表示平面的平行四边形的一边垂直, 如图 8.6-9 所示.
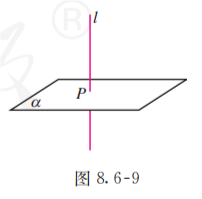
思考
在同一平面内, 过一点有且只有一条直线与已知直线垂直. 将这一结论推广到空间, 过一点垂直于已知平面的直线有几条? 为什么?
定理
可以发现, 过一点垂直于已知平面的直线有且只有一条.
定义
过一点作垂直于已知平面的直线, 则该点与垂足间的线段, 叫做这个点到该平面的垂线段, 垂线段的长度叫做这个点到该平面的距离.
例子
在棱锥的体积公式中, 棱锥的高就是棱锥的顶点到底面的距离.
下面我们来研究直线与平面垂直的判定, 即探究直线与平面垂直的充分条件.
根据定义可以进行判断, 但无法验证一条直线与一个平面内的所有直线都垂直. 那么, 有没有可行的方法?
探究
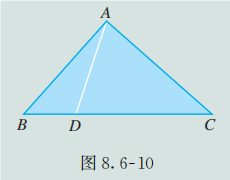
如图 8.6-10, 准备一块三角形的纸片 , 过 的顶点 翻折纸片, 得到折痕 , 将翻折后的纸片坚起放置在桌面上 ( 与桌面接触).
(1) 折痕 与桌面垂直吗?
(2) 如何翻折才能使折痕 与桌面垂直? 为什么?
容易发现, 所在直线与桌面所在平面 垂直(图 8.6-11)的充要条件是折痕 是 边上的高. 这时, 由于翻折之后垂直关系不变, 所以直线 与平面 内的两条相交直线 都垂直.
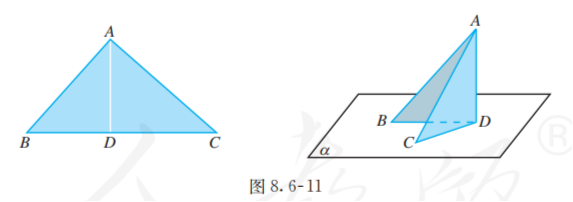
事实上, 由基本事实的推论 2, 平面 可以看作由两条相交直线 所唯一确定的, 所以当直线 垂直于这两条相交直线时, 就能保证直线 与 内所有直线都垂直.
一般地, 我们有如下判定直线与平面垂直的定理.
定理
如果一条直线与一个平面内的两条相交直线垂直, 那么该直线与此平面垂直.
它可以用符号表示为:
定理体现了 “直线与平面垂直” 和 “直线与直线垂直”的互相转化.
思考
两条相交直线可以确定一个平面, 两条平行直线也可以确定一个平面, 那么定理中的 “两条相交直线” 可以改为 “两条平行直线” 吗? 你能从向量的角度解释原因吗? 如果改为 “无数条直线” 呢?
例 3
求证: 如果两条平行直线中的一条直线垂直于一个平面, 那么另一条直线也垂直于这个平面.
已知: 如图 8.6-12, , 求证 .
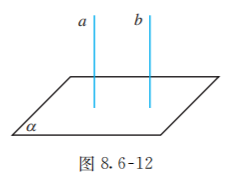
分析:
要证明直线 , 根据直线与平面垂直的判定定理可知, 只需证明直线 垂直于平面 内的两条相交直线即可.
证明:
如图 8.6-13, 在平面 内取两条相交直线 .
直线 ,
.
,
.
又 是两条相交直线,
.
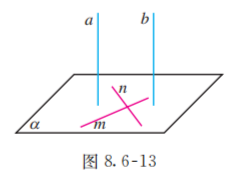
思考
你能用直线与平面垂直的定义证明这个结论吗?
定义 直线和平面所成角
如图 8.6-14, 一条直线 与一个平面 相交, 但不与这个平面垂直, 这条直线叫做这个平面的斜线, 斜线和平面的交点 叫做斜足. 过斜线上斜足以外的一点 向平面 引垂线 , 过垂足 和斜足 的直线 叫做斜线在这个平面上的射影. 平面的一条斜线和它在平面上的射影所成的角, 叫做这条直线和这个平面所成的角.
一条直线垂直于平面,我们说它们所成的角是 ;一条直线和平面平行,或在平面内,我们说它们所成的角是 。直线与平面所成的角 的取值范围是 .
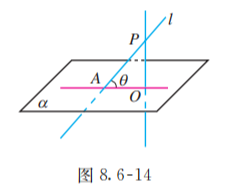
思考
如果 是平面 内的任意一条不与直线 重合的直线, 那么直线 与直线 所成的角和直线 与这个平面所成的角的大小关系是什么?
例 4
如图 8.6-15,在正方体 中,求直线 和平面 所成的角。
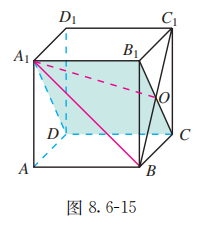
分析:
关键是找出直线 在平面 上的射影。
解:
连接 与 相交于点 ,连接 。设正方体的棱长为 。
,
平面 .
.
又 ,
平面 .
为斜线 在平面 上的射影, 为 和平面 所成的角.
在 Rt 中, ,
.
.
直线 和平面 所成的角为 .