1.5 充分条件与必要条件
2024-01-07 23:12:05 新建
在初中, 我们已经对命题有了初步的认识. 一般地, 我们把用语言、符号或式子表达的, 可以判断真假的陈述句叫做命题. 判断为真的语句是真命题, 判断为假的语句是假命题. 中学数学中的许多命题可以写成 “若 , 则 ” “如果 ,那么 ” 等形式. 其中 称为命题的条件, 称为命题的结论. 本节主要讨论这种形式的命题. 下面我们将进一步考察 “若 , 则 ” 形式的命题中 和 的关系, 学习数学中的三个常用的逻辑用语————充分条件、必要条件和充要条件.
1.5.1 充分条件与必要条件
思考
下列 “若 , 则 ” 形式的命题中, 哪些是真命题? 哪些是假命题?
(1) 若平行四边形的对角线互相垂直, 则这个平行四边形是菱形;
(2) 若两个三角形的周长相等, 则这两个三角形全等;
(3) 若 , 则 ;
(4) 若平面内两条直线 和 均垂直于直线 , 则 .
在命题 (1) (4) 中, 由条件 通过推理可以得出结论 , 所以它们是真命题. 在命题 (2) (3) 中, 由条件 不能得出结论 , 所以它们是假命题.
定义
一般地, “ 若 , 则 ” 为真命题, 是指由 通过推理可以得出 . 这时, 我们就说, 由 可以推出 , 记作
并且说, 是 的充分条件 (sufficient condition), 是 的必要条件 (necessary condition).
当 是 的必要条件, 如果 不成立, 则 一定不成立. 所以, 对于 成立而言是必要的. 请举例说明.
定义
如果 “若 , 则 ” 为假命题, 那么由条件 不能推出结论 , 记作 . 此时, 我们就说 不是 的充分条件, 不是 的必要条件.
上述命题 (1) (4) 中的 是 的充分条件, 是 的必要条件, 而命题 (2) (3) 中的 不是 的充分条件, 不是 的必要条件.
例 1
下列 “若 , 则 ” 形式的命题中, 哪些命题中的 是 的充分条件?
(1) 若四边形的两组对角分别相等, 则这个四边形是平行四边形;
(2) 若两个三角形的三边成比例, 则这两个三角形相似;
(3) 若四边形为菱形, 则这个四边形的对角线互相垂直;
(4) 若 , 则 ;
(5) 若 , 则 ;
(6) 若 为无理数, 则 为无理数.
解:
(1) 这是一条平行四边形的判定定理, , 所以 是 的充分条件.
(2) 这是一条相似三角形的判定定理, , 所以 是 的充分条件.
(3) 这是一条菱形的性质定理, , 所以 是 的充分条件.
(4) 由于 , 但 , 所以 不是 的充分条件.
(5) 由等式的性质知, , 所以 是 的充分条件.
(6) 为无理数, 但 为有理数, , 所以 不是 的充分条件.
举反例是判断一个命题是假命题的重要方法.
思考
例 1 中命题(1)给出了 “四边形是平行四边形” 的一个充分条件, 即 “四边形的两组对角分别相等”. 这样的充分条件唯一吗? 如果不唯一, 那么你能再给出几个不同的充分条件吗?
我们说 是 的充分条件, 是指由条件 可以推出结论 , 但这并不意味着只能由这个条件 才能推出结论 . 一般来说, 对给定结论 , 使得 成立的条件 是不唯一的.例如, 我们知道, 下列命题均为真命题:
(1)若四边形的两组对边分别相等, 则这个四边形是平行四边形;
(2)若四边形的一组对边平行且相等, 则这个四边形是平行四边形;
(3)若四边形的两条对角线互相平分, 则这个四边形是平行四边形.
所以, “四边形的两组对边分别相等” “四边形的一组对边平行且相等” “四边形的两条对角线互相平分” 都是 “四边形是平行四边形” 的充分条件.
事实上, 例 1 中命题 (1) 及上述命题(1)(2)(3)均是平行四边形的判定定理. 所以, 平行四边形的每一条判定定理都给出了 “四边形是平行四边形” 的一个充分条件, 即这个条件能充分保证四边形是平行四边形. 类似地, 平行线的每一条判定定理都给出了 “两直线平行” 的一个充分条件, 例如 “内错角相等” 这个条件就充分保证了 “两条直线平行”.
一般地, 数学中的每一条判定定理都给出了相应数学结论成立的一个充分条件.
例 2
下列 “若 , 则 ” 形式的命题中, 哪些命题中的 是 的必要条件?
(1) 若四边形为平行四边形, 则这个四边形的两组对角分别相等;
(2) 若两个三角形相似, 则这两个三角形的三边成比例;
(3) 若四边形的对角线互相垂直, 则这个四边形是菱形;
(4) 若 , 则 ;
(5) 若 , 则 ;
(6) 若 为无理数, 则 为无理数.
解:
(1) 这是平行四边形的一条性质定理, , 所以, 是 的必要条件.
(2) 这是三角形相似的一条性质定理, , 所以, 是 的必要条件.
(3) 如图 1.4-1, 四边形 的对角线互相垂直,但它不是菱形, , 所以, 不是 的必要条件.
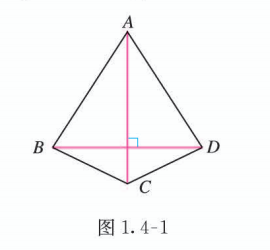
(4) 显然, , 所以, 是 的必要条件.
(5) 由于 , 但 , 所以, 不是 的必要条件.
(6) 由于 为无理数, 但 不全是无理数, , 所以, 不是 的必要条件.
一般地, 要判断 “若 , 则 ” 形式的命题中 是否为 的必要条件, 只需判断是否有 “ ”, 即 “若 , 则 ” 是否为真命题.
思考
例 2 中命题(1)给出了 “四边形是平行四边形” 的一个必要条件, 即 “这个四边形的两组对角分别相等”. 这样的必要条件是唯一的吗? 如果不唯一, 你能给出 “四边形是平行四边形”的几个其他必要条件吗?
我们说 是 的必要条件, 是指以 为条件可以推出结论 , 但这并不意味着由条件 只能推出结论 .一般来说, 给定条件 , 由 可以推出的结论 是不唯一的. 例如,下列命题都是真命题:
(1)若四边形是平行四边形, 则这个四边形的两组对边分别相等;
(2)若四边形是平行四边形, 则这个四边形的一组对边平行且相等;
(3)若四边形是平行四边形, 则这个四边形的两条对角线互相平分.
这表明, “四边形的两组对边分别相等” “四边形的一组对边平行且相等” “四边形的两条对角线互相平分” 都是 “四边形是平行四边形” 的必要条件.
我们知道, 例 2 中命题 (1)及上述命题(1)(2)(3)均为平行四边形的性质定理. 所以, 平行四边形的每条性质定理都给出了 “四边形是平行四边形” 的一个必要条件. 类似地, 平行线的每条性质定理都给出了 “两直线平行” 的一个必要条件,例如 “同位角相等” 是 “两直线平行” 的必要条件, 也就是说, 如果同位角不相等, 那么就不可能有 “两直线平行”.
一般地, 数学中的每一条性质定理都给出了相应数学结论成立的一个必要条件.
练习
1.
下列 “若 , 则 ” 形式的命题中, 哪些命题中的 是 的充分条件?
(1) 若平面内点 在线段 的垂直平分线上, 则 ;
(2) 若两个三角形的两边及一边所对的角分别相等, 则这两个三角形全等;
(3) 若两个三角形相似, 则这两个三角形的面积比等于周长比的平方.
2.
下列 “若 , 则 ” 形式的命题中, 哪些命题中的 是 的必要条件?
(1) 若直线 与 有且仅有一个交点, 则 为 的一条切线;
(2) 若 是无理数, 则 也是无理数.
3.
如图, 直线 与 被直线 所截, 分别得到了 和 . 请根据这些信息, 写出几个 “ ” 的充分条件和必要条件.
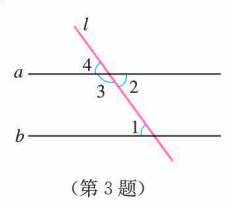
1.4.2 充要条件
定义 逆命题
将命题 “若 , 则 ”中的条件 和结论 互换, 就得到一个新的命题 “若 , 则 ”, 称这个命题为原命题的逆命题.
思考
下列 “若 , 则 ” 形式的命题中, 哪些命题与它们的逆命题都是真命题?
(1) 若两个三角形的两角和其中一角所对的边分别相等, 则这两个三角形全等;
(2) 若两个三角形全等, 则这两个三角形的周长相等;
(3) 若一元二次方程 有两个不相等的实数根, 则 ;
(4) 若 是空集, 则 与 均是空集.
不难发现, 上述命题中的命题 (1) (4) 和它们的逆命题都是真命题; 命题 (2) 是真命题, 但它的逆命题是假命题;命题 (3) 是假命题, 但它的逆命题是真命题.
定义 充要条件
如果 “若 , 则 ” 和它的逆命题 “若 , 则 ” 均是真命题, 即既有 , 又有 , 就记作
此时, 既是 的充分条件, 也是 的必要条件, 我们说 是 的充分必要条件, 简称为充要条件 (necessary and sufficient condition). 显然, 如果 是 的充要条件, 那么 也是 的充要条件.
概括地说, 如果 , 那么 与 互为充要条件.
上述命题 (1) (4) 中的 与 互为充要条件.
例 3
下列各题中, 哪些 是 的充要条件?
(1) : 四边形是正方形, : 四边形的对角线互相垂直且平分;
(2) : 两个三角形相似, : 两个三角形三边成比例;
(3) ;
(4) 是一元二次方程 的一个根, .
解:
(1) 因为对角线互相垂直且平分的四边形不一定是正方形 (为什么), 所以 , 所以 不是 的充要条件.
(2) 因为 “若 , 则 ” 是相似三角形的性质定理, “若 , 则 ” 是相似三角形的判定定理, 所以它们均为真命题, 即 , 所以 是 的充要条件.
(3) 因为 时, 不一定成立 (为什么), 所以 , 所以 不是 的充要条件.
(4) 因为 “若 , 则 ” 与 “若 , 则 ” 均为真命题, 即 , 所以 是 的充要条件.
探究
通过上面的学习, 你能给出 “四边形是平行四边形”的充要条件吗?
过程
可以发现,“四边形的两组对角分别相等” “四边形的两组对边分别相等” “四边形的一组对边平行且相等” 和 “四边形的对角线互相平分” 既是 “四边形是平行四边形” 的充分条件, 又是必要条件, 所以它们都是 “四边形是平行四边形” 的充要条件.
另外, 我们再看平行四边形的定义: 两组对边分别平行的四边形叫做平行四边形, 它表明 “四边形的两组对边分别平行” 也是 “四边形是平行四边形” 的一个充要条件.
上面的这些充要条件从不同角度刻画了 “平行四边形” 这个概念, 据此我们可以给出平行四边形的其他定义形式. 例如:
两组对边分别相等的四边形叫做平行四边形;
对角线互相平分的四边形叫做平行四边形.
类似地, 利用 “两个三角形全等” 的充要条件, 可以给出 “三角形全等” 的其他定义形式, 而且这些定义是相互等价的; 同样, 利用 “两个三角形相似” 的充要条件, 可以给出 “相似三角形” 其他定义形式, 这些定义也是相互等价的; 等等.
例 4
已知: 的半径为 , 圆心 到直线 的距离为 . 求证: 是直线 与 相切的充要条件.
分析:
设 直线 与 相切. 要证 是 的充要条件, 只需分别证明充分性 和必要性 即可.
证明:
设 直线 与 相切.
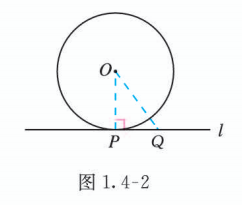
(1) 充分性 : 如图 1.4-2, 作 于点 , 则 . 若 , 则点 在 上. 在直线 上任取一点 (异于点 ), 连接 . 在 Rt 中, . 所以,除点 外直线 上的点都在 的外部, 即直线 与 仅有一个公共点 . 所以直线 与 相切.
(2) 必要性 : 若直线 与 相切, 不妨设切点为 , 则 . 因此, .
由 (1) (2) 可得, 是直线 与 相切的充要条件.
练习
1.
下列各题中, 哪些 是 的充要条件?
(1) : 三角形为等腰三角形, : 三角形存在两角相等;
(2) 内两条弦相等, 内两条弦所对的圆周角相等;
(3) 为空集, 与 之一为空集.
2.
分别写出 “两个三角形全等” 和 “两个三角形相似” 的几个充要条件.
3.
证明: 如图, 梯形 为等腰梯形的充要条件为 .

习题 1.4
复习巩固
1.
举例说明:
(1) 是 的充分不必要条件;
(2) 是 的必要不充分条件;
(3) 是 的充要条件.
2.
在下列各题中, 判断 是 的什么条件(请用 “充分不必要条件” “必要不充分条件” “充要条件” “既不充分也不必要条件” 回答):
(1) : 三角形是等腰三角形, : 三角形是等边三角形;
(2) : 一元二次方程 有实数根, ;
(3) ;
(4) ;
(5) .
3.
判断下列命题的真假:
(1) 点 到圆心 的距离大于圆的半径是点 在 外的充要条件;
(2) 两个三角形的面积相等是这两个三角形全等的充分不必要条件;
(3) 是 的必要不充分条件;
(4) 或 为有理数是 为有理数的既不充分也不必要条件.
综合运用
4.
已知 满足条件 满足条件 ,
(1) 如果 , 那么 是 的什么条件?
(2) 如果 , 那么 是 的什么条件?
(3) 如果 , 那么 是 的什么条件?
5.
设 . 证明: 的充要条件是 .
拓广探索
6.
设 分别是 的三条边, 且 . 我们知道, 如果 为直角三角形, 那么 (勾股定理). 反过来, 如果 , 那么 为直角三角形 (勾股定理的逆定理). 由此可知, 为直角三角形的充要条件是 .请利用边长 分别给出 为锐角三角形和钝角三角形的一个充要条件, 并证明.