5.3 诱导公式

2024-03-22 22:18:38 新建

前面利用圆的几何性质, 得到了同角三角函数之间的基本关系. 我们知道, 圆的最重要的性质是对称性, 而对称性 (如奇偶性) 也是函数的重要性质. 由此想到, 可以利用圆的对称性, 研究三角函数的对称性.

探究 1

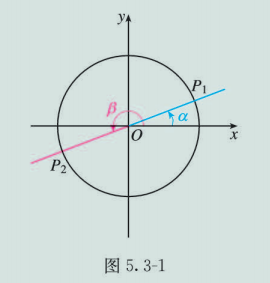
如图 5.3-1, 在直角坐标系内, 设任意角 $α$ 的终边与单位圆交于点 $P_{1}$ .
(1) 作 $P_{1}$ 关于原点的对称点 $P_{2}$ , 以 $O P_{2}$ 为终边的角 $β$ 与角 $α$ 有什么关系? 角 $β, α$ 的三角函数值之间有什么关系?
(2) 如果作 $P_{1}$ 关于 $x$ 轴（或 $y$ 轴）的对称点 $P_{3}$ (或 $P_{4}$ ), 那么又可以得到什么结论?

探究

下面, 借助单位圆的对称性进行探究.

如图 5.3-2, 以 $O P_{2}$ 为终边的角 $β$ 都是与角 $π + α$ 终边相同的角, 即 $β = 2 kπ + (π + α) (k \in Z)$ . 因此,只要探究角 $π + α$ 与 $α$ 的三角函数值之间的关系即可.

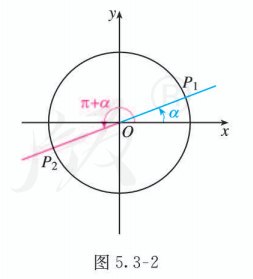
设 $P_{1} (x_{1}, y_{1}), P_{2} (x_{2}, y_{2})$ . 因为 $P_{2}$ 是点 $P_{1}$ 关于原点的对称点, 所以

$x_{2} = - x_{1}, y_{2} = - y_{1} .$

根据三角函数的定义, 得

$sin α = y_{1}, cos α = x_{1}, tan α = \frac{y _{1}}{x _{1}}; sin (π + α) = y_{2}, cos (π + α) = x_{2}, tan (π + α) = \frac{y _{2}}{x _{2}} .$

从而得

公式二

$sin (π + α) = - sin α, cos (π + α) = - cos α, tan (π + α) = tan α .$

如图 5.3-3, 作 $P_{1}$ 关于 $x$ 轴的对称点 $P_{3}$ , 则以 $O P_{3}$ 为终边的角为 $- α$ , 并且有

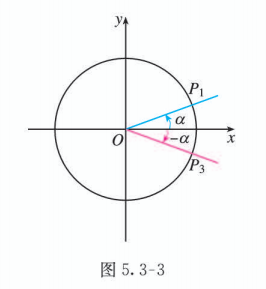
公式三

$sin (- α) = - sin α, cos (- α) = cos α, tan (- α) = - tan α .$

如图 5.3-4, 作 $P_{1}$ 关于 $y$ 轴的对称点 $P_{4}$ , 则以 $O P_{4}$ 为终边的角为 $π - α$ , 并且有

公式四

$sin (π - α) = sin α, cos (π - α) = - cos α, tan (π - α) = - tan α .$

角 $π + α$ 还可以看作是角 $α$ 的终边按逆时针方向旋转角 $π$ 得到的.

思考

请你类比公式二, 证明公式三和公式四.

例 1

利用公式求下列三角函数值:
(1) $cos 22 5^{\circ}$ ;
(2) $sin \frac{8 π}{3}$ ;
(3) $sin (- \frac{16 π}{3})$ ;
(4) $tan (- 204 0^{\circ})$ .

解:

(1)

$cos 22 5^{\circ} = cos (18 0^{\circ} + 4 5^{\circ}) = - cos 4 5^{\circ} = - \frac{2}{2};$

(2)

$sin \frac{8 π}{3} = sin (2 π + \frac{2 π}{3}) = sin \frac{2 π}{3} = sin (π - \frac{π}{3}) = sin \frac{π}{3} = \frac{3}{2}$

(3)

$sin (- \frac{16 π}{3}) = - sin \frac{16 π}{3} = - sin (5 π + \frac{π}{3}) = - (- sin \frac{π}{3}) = \frac{3}{2};$

(4)

$tan (- 204 0^{\circ}) = - tan 204 0^{\circ} = - tan (6 \times 36 0^{\circ} - 12 0^{\circ}) = tan 12 0^{\circ} = tan (18 0^{\circ} - 6 0^{\circ}) = - tan 6 0^{\circ} = - 3 .$

思考

由例 1, 你对公式一 $\sim$ 公式四的作用有什么进一步的认识? 你能自己归纳一下把任意角的三角函数转化为锐角三角函数的步骤吗?

利用公式一 $\sim$ 公式四, 可以把任意角的三角函数转化为锐角三角函数, 一般可按下面步骤进行:

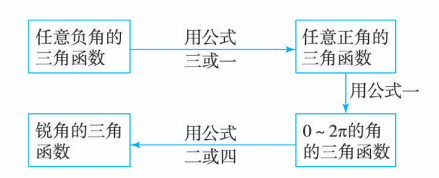
数学史上, 求三角函数值曾经是一个重要而困难的问题. 数学家制作了锐角三角函数表, 并通过公式一 $\sim$ 公式四, 按上述步骤解决了问题. 现在, 我们可以利用计算工具方便地求任意角的三角函数值, 所以这些公式的 “求值” 作用已经不重要了, 但它们所体现的三角函数的对称性, 在解决三角函数的各种问题中却依然有重要的作用.

例 2

化简

$\frac{cos ( 18 0 ^{\circ} + α ) sin ( α + 36 0 ^{\circ} )}{tan ( - α - 18 0 ^{\circ} ) cos ( - 18 0 ^{\circ} + α )} .$

解:

$tan (- α - 18 0^{\circ}) cos (- 18 0^{\circ} + α) = tan [- (18 0^{\circ} + α)] = - tan (18 0^{\circ} + α) = - tan α = cos [- (18 0^{\circ} - α)] = cos (18 0^{\circ} - α) = - cos α$

所以

$原式 = \frac{- cos α sin α}{( - tan α ) ( - cos α )} = - cos α .$

练习

将下列三角函数转化为锐角三角函数, 并填在题中横线上:
(1) $cos \frac{13}{9} π =$
(2) $sin (1 + π) =$
(3) $sin (- \frac{π}{5}) =$
(4) $tan (- 7 0^{\circ} 6^{'}) =$
(5) $cos \frac{6 π}{7} =$
(6) $tan 100 0^{\circ} 2 1^{'} =$

利用公式求下列三角函数值:
(1) $cos (- 42 0^{\circ})$ ;
(2) $sin (- \frac{7}{6} π)$ ;
(3) $tan (- 114 0^{\circ})$ ;
(4) $cos (- \frac{77}{6} π)$ ;
(5) $tan 31 5^{\circ}$ ;
(6) $sin (- \frac{11}{4} π)$ .

化简:
(1) $sin (- α - 18 0^{\circ}) cos (- α) sin (- α + 18 0^{\circ})$ ;
(2) $cos^{3} (- α) sin (2 π + α) tan^{3} (- α - π)$ .

填表:

$α$	$- \frac{4 π}{3}$	$- \frac{5 π}{4}$	$- \frac{5 π}{3}$	$- \frac{7 π}{4}$	$- \frac{8 π}{3}$	$- \frac{11 π}{4}$
$sin α$
$cos α$
$tan α$

下面在探究 1 的基础上继续探究.

探究 2

作 $P_{1}$ 关于直线 $y = x$ 的对称点 $P_{5}$ , 以 $O P_{5}$ 为终边的角 $γ$ 与角 $α$ 有什么关系? 角 $γ$ 与角 $α$ 的三角函数值之间有什么关系?

解

如图 5.3-5, 以 $O P_{5}$ 为终边的角 $γ$ 都是与角 $\frac{π}{2} - α$ 终边相同的角, 即 $γ = 2 kπ + (\frac{π}{2} - α)$ $(k \in Z)$ . 因此, 只要探究角 $\frac{π}{2} - α$ 与 $α$ 的三角函数值之间的关系即可.

设 $P_{5} (x_{5}, y_{5})$ , 由于 $P_{5}$ 是点 $P_{1}$ 关于直线 $y = x$ 的对称点, 可以证明

$x_{5} = y_{1}, y_{5} = x_{1} . (1)$

思考

你能利用平面几何的知识, 就图 5.3-5 所示的情况证明(1)式吗? 其他情况呢?

解

根据三角函数的定义, 得

$sin (\frac{π}{2} - α) = y_{5}, cos (\frac{π}{2} - α) = x_{5} .$

从而得

公式五

$sin (\frac{π}{2} - α) = cos α, cos (\frac{π}{2} - α) = sin α .$

探究 3

作 $P_{5}$ 关于 $y$ 轴的对称点, 又能得到什么结论?

解

类似地, 可得

公式六

$sin (\frac{π}{2} + α) = cos α, cos (\frac{π}{2} + α) = - sin α .$

思考

角 $\frac{π}{2} + α$ 的终边与角 $α$ 的终边具有怎样的对称性? 据此你将如何证明公式六?

利用公式五或公式六, 可以实现正弦函数与余弦函数的相互转化.
公式一～公式六都叫做诱导公式.

例 3

证明:
(1) $sin (\frac{3 π}{2} - α) = - cos α$ ;
(2) $cos (\frac{3 π}{2} + α) = sin α$ .

证明:

(1)

$sin (\frac{3 π}{2} - α) = sin [π + (\frac{π}{2} - α)] = - sin (\frac{π}{2} - α) = - cos α;$

(2)

$cos (\frac{3 π}{2} + α) = cos [π + (\frac{π}{2} + α)] = - cos (\frac{π}{2} + α) = sin α .$

例 4

化简

$\frac{sin ( 2 π - α ) cos ( π + α ) cos ( \frac{π}{2} + α ) cos ( \frac{11 π}{2} - α )}{cos ( π - α ) sin ( 3 π - α ) sin ( - π - α ) sin ( \frac{9 π}{2} + α )} .$

解：

原式

$= \frac{( - sin α ) ( - cos α ) ( - sin α ) cos [ 5 π + ( \frac{π}{2} - α ) ]}{( - cos α ) sin ( π - α ) [ - sin ( π + α )] sin [ 4 π + ( \frac{π}{2} + α ) ]} = \frac{- sin ^{2} α cos α [ - cos ( \frac{π}{2} - α ) ]}{( - cos α ) sin α [ - ( - sin α )] sin ( \frac{π}{2} + α )} = - \frac{sin α}{cos α} = - tan α .$

例 5

已知 $sin (5 3^{\circ} - α) = \frac{1}{5}$ , 且 $- 27 0^{\circ} < α < - 9 0^{\circ}$ , 求 $sin (3 7^{\circ} + α)$ 的值.

分析:

联系条件与结论, 注意到 $(5 3^{\circ} - α) + (3 7^{\circ} + α) = 9 0^{\circ}$ , 由此可利用诱导公式解决问题.

解:

因为 $(5 3^{\circ} - α) + (3 7^{\circ} + α) = 9 0^{\circ}$ , 所以由诱导公式五, 得

$sin (3 7^{\circ} + α) = sin [9 0^{\circ} - (5 3^{\circ} - α)] = cos (5 3^{\circ} - α)$

因为

$- 27 0^{\circ} < α < - 9 0^{\circ},$

所以

$14 3^{\circ} < 5 3^{\circ} - α < 32 3^{\circ} .$

由 $sin (5 3^{\circ} - α) = \frac{1}{5} > 0$ , 得 $14 3^{\circ} < 5 3^{\circ} - α < 18 0^{\circ}$ .
所以

$cos (5 3^{\circ} - α) = - 1 - sin^{2} (5 3^{\circ} - α) = - 1 - (\frac{1}{5})^{2} = - \frac{2 6}{5},$

所以

$sin (3 7^{\circ} + α) = - \frac{2 6}{5} .$

练习

用诱导公式求下列三角函数值 (可用计算工具, 第 (3) (4) (6)题精确到 0.000 1):
(1) $cos \frac{65}{6} π$ ;
(2) $sin (- \frac{31}{4} π)$ ;
(3) $cos (- 118 2^{\circ} 1 3^{'})$ ;
(4) $sin 67 0^{\circ} 3 9^{'}$ ;
(5) $tan (- \frac{26 π}{3})$ ;
(6) $tan 58 0^{\circ} 2 1^{'}$ .

证明:
(1) $cos (\frac{5}{2} π - α) = sin α$ ;
(2) $cos (\frac{7}{2} π + α) = sin α$ ;
(3) $sin (\frac{9}{2} π - α) = cos α$ ;
(4) $sin (\frac{11}{2} π - α) = - cos α$ .

化简:
(1) $\frac{cos ( α - \frac{π}{2} )}{sin ( \frac{5 π}{2} + α )} sin (α - 2 π) cos (2 π - α)$ ;
(2) $cos^{2} (- α) - \frac{tan ( 2 π + α )}{cos ( \frac{π}{2} + α )}$ ;
(3) $\frac{cos ( α - 3 π ) cos ( \frac{3 π}{2} - α )}{sin ^{2} ( α - \frac{π}{2} )}$ .

习题 5.3

复习巩固

用诱导公式求下列三角函数值（可用计算工具, 第 (2)(3)(4)(5)题精确到 0.000 1):
(1) $cos (- \frac{17 π}{4})$ ;
(2) $sin (- 157 4^{\circ})$ ;
(3) $sin (- 216 0^{\circ} 5 2^{'})$ ;
(4) $cos (- 175 1^{\circ} 3 6^{'})$ ;
(5) $cos 161 5^{\circ} 8^{'}$ ;
(6) $sin (- \frac{26}{3} π)$ .

求证:
(1) $sin (36 0^{\circ} - α) = - sin α$ ;
(2) $cos (36 0^{\circ} - α) = cos α$ ;
(3) $tan (36 0^{\circ} - α) = - tan α$ .

化简 :
(1) $1 + sin (α - 2 π) sin (π + α) - 2 cos^{2} (- α)$ ;
(2) $sin (- 107 1^{\circ}) sin 9 9^{\circ} + sin (- 17 1^{\circ}) sin (- 26 1^{\circ})$ .

在单位圆中, 已知角 $α$ 的终边与单位圆的交点为 $P (- \frac{3}{5}, \frac{4}{5})$ , 分别求角 $π + α, - α, \frac{π}{2} + α$ 的正弦、余弦函数值.

综合运用

已知 $sin (\frac{7 π}{2} + α) = \frac{3}{5}$ , 那么 $cos α =$ ( ).
(A) $- \frac{4}{5}$
(B) $- \frac{3}{5}$
(C) $\frac{3}{5}$
(D) $\frac{4}{5}$

已知 $sin (π + α) = - \frac{1}{2}$ , 计算:
(1) $sin (5 π - α)$ ;
(2) $sin (\frac{π}{2} + α)$ ;
(3) $cos (α - \frac{3 π}{2})$ ;
(4) $tan (\frac{π}{2} - α)$ .

在 $△ A BC$ 中, 试判断下列关系是否成立, 并说明理由.
(1) $cos (A + B) = cos C$ ;
(2) $sin (A + B) = sin C$ ;
(3) $sin \frac{A + B}{2} = sin \frac{C}{2}$ ;
(4) $cos \frac{A + B}{2} = cos \frac{C}{2}$ .

已知 $sin (\frac{π}{3} - x) = \frac{1}{3}$ , 且 $0 < x < \frac{π}{2}$ , 求 $sin (\frac{π}{6} + x)$ 和 $cos (\frac{2 π}{3} + x)$ 的值.

拓广探索

化简下列各式, 其中 $n \in Z$ :
(1) $sin (\frac{nπ}{2} + α)$ ;
(2) $cos (\frac{nπ}{2} - α)$ .

10.

借助单位圆, 还可以建立角的终边之间的哪些特殊位置关系? 由此还能得到三角函数值之间的哪些恒等关系?