4.5 函数的应用(二)
2024-02-24 22:20:44 新建
在 “函数的应用 (一) ”中, 通过一些实例, 我们初步了解了建立函数模型解决实际问题的过程, 学习了用函数描述客观事物变化规律的方法. 本节将先学习运用函数性质求方程近似解的基本方法(二分法),再结合实例,更深入地理解用函数构建数学模型的基本过程, 学习运用模型思想发现和提出问题、分析和解决问题的方法.
4.5.1 函数的零点与方程的解
思考
我们已经学习了用二次函数的观点认识一元二次方程, 知道一元二次方程的实数根就是相应二次函数的零点. 像 这样不能用公式求解的方程, 是否也能采用类似的方法, 用相应的函数研究它的解的情况呢?
定义 零点
与二次函数的零点一样, 对于一般函数 , 我们把使 的实数 叫做函数 的零点 (zero).
定理 方程有实数解的等价条件
这样, 函数 的零点就是方程 的实数解, 也就是函数 的图象与 轴的公共点的横坐标. 所以
方程 有实数解
函数 有零点
函数 的图象与 轴有公共点.
由此可知, 求方程 的实数解, 就是确定函数 的零点. 一般地, 对于不能用公式求解的方程 , 我们可以把它与相应的函数 联系起来, 利用函数的图象和性质找出零点, 从而得到方程的解.
下面从考察二次函数存在零点时函数图象的特征, 以及零点附近函数值的变化规律人手.
探究
对于二次函数 , 观察它的图象 (图 4.5-1),发现它在区间 上有零点. 这时, 函数图象与 轴有什么关系? 在区间 上是否也有这种关系? 你认为应如何利用函数 的取值规律来刻画这种关系?
再任意画几个函数的图象, 观察函数零点所在区间, 以及这一区间内函数图象与 轴的关系, 并探究用 的取值刻画这种关系的方法.

解
可以发现, 在零点附近, 函数图象是连续不断的, 并且 “穿过” 轴. 函数在端点 和 的取值异号, 即 , 函数 在区间 内有零点 , 它是方程 的一个根. 同样地, , 函数 在 内有零点 , 它是方程 的另一个根.
一般地, 我们有:
定理 函数零点存在定理
如果函数 在区间 上的图象是一条连续不断的曲线, 且有 , 那么, 函数 在区间 内至少有一个零点, 即存在 , 使得 , 这个 也就是方程 的解.
例 1
求方程 的实数解的个数.
分析:
可以先借助计算工具画出函数 的图象或列出 的对应值表, 为观察、判断零点所在区间提供帮助.
解:
设函数 , 利用计算工具, 列出函数 的对应值表 (表 4.5-1), 并画出图象(图 4.5-2).

由表 4.5-1 和图 4.5-2 可知, , 则 . 由函数零点存在定理可知, 函数 在区间 内至少有一个零点.
容易证明, 函数 是增函数, 所以它只有一个零点, 即相应方程 只有一个实数解.
思考
为什么由图 4.5-2 和 还不能说明函数 只有一个零点? 你能证明函数 是增函数吗?
练习
1.
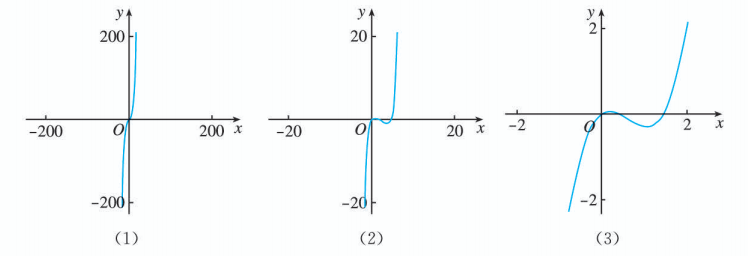
图 (1) (2) (3) 分别为函数 在三个不同范围的图象. 能否仅根据其中一个图象, 得出函数 在某个区间只有一个零点的判断? 为什么?
2.
利用计算工具画出函数的图象, 并指出下列函数零点所在的大致区间:
(1) ;
(2) ;
(3) ;
(4) .
4.5.2 用二分法求方程的近似解
探究
我们已经知道, 函数 在区间 内存在一个零点. 进一步的问题是, 如何求出这个零点呢?
大多数方程都不能像一元二次方程那样用公式求出精确解. 在实际问题中, 往往只需求出满足一定精确度的近似解.
定义 中点
一般地, 称 为区间 的中点.
解
一个直观的想法是: 如果能将零点所在的范围尽量缩小, 那么在一定精确度的要求下, 就可以得到符合要求的零点的近似值. 为了方便, 可以通过取区间中点的方法, 逐步缩小零点所在的范围.
取区间 的中点 , 用计算工具算得 . 因为 , 所以零点在区间 内.
再取区间 的中点 , 用计算工具算得 . 因为 ,所以零点在区间 内.
由于 , 所以零点所在的范围变小了. 如果重复上述步骤, 那么零点所在的范围会越来越小(如表 4.5-2 和图 4.5-3). 这样, 我们就可以通过有限次重复相同的步骤, 将零点所在范围缩小到满足一定精确度的区间, 区间内的任意一点都可以作为函数零点的近似值. 为了方便, 我们把区间的一个端点作为零点的近似值.
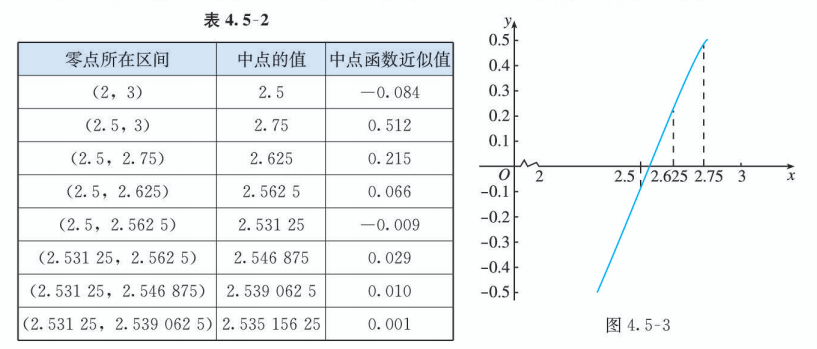
例如, 当精确度为 时, 因为 , 所以区间 内任意一点都可以作为零点的近似值, 也可以将 作为函数 零点的近似值, 也即方程 的近似解.
二分法
对于在区间 上图象连续不断且 的函数 , 通过不断地把它的零点所在区间一分为二, 使所得区间的两个端点逐步逼近零点, 进而得到零点近似值的方法叫做二分法 (bisection method).
求函数零点的近似值
给定精确度 , 用二分法求函数 零点 的近似值的一般步骤如下:
- 确定零点 的初始区间 , 验证 .
- 求区间 的中点 .
- 计算 , 并进一步确定零点所在的区间:
(1) 若 (此时 ), 则 就是函数的零点;
(2) 若 (此时 ), 则令 ;
(3) 若 (此时 ), 则令 . - 判断是否达到精确度 : 若 , 则得到零点近似值 (或 ); 否则重复步骤 .
思考
为了刻画与准确值的接近程度, 这里给出了精确度 , 由 可知, 区间 中任意一个值都是零点 满足精确度 的近似值(想一想,为什么)。
由函数零点与相应方程解的关系, 我们可用二分法来求方程的近似解.
例 2
借助信息技术, 用二分法求方程 的近似解 (精确度为 ).
解:
原方程即 , 令 , 用信息技术画出函数 的图象 (图 4.5-4), 并列出它的对应值表(表 4.5-3).
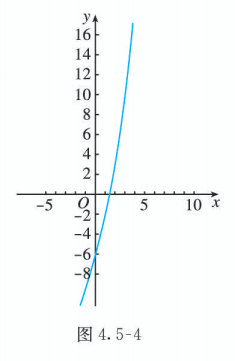
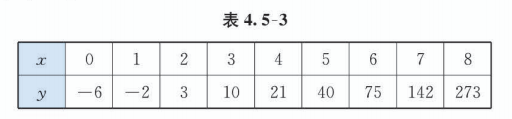
观察图 4.5-4 或表 4.5-3, 可知 , 说明该函数在区间 内存在零点 .
取区间 的中点 , 用信息技术算得 . 因为 , 所以 .
再取区间 的中点 , 用信息技术算得 . 因为 ,所以 .
同理可得, .由于
所以, 原方程的近似解可取为 .
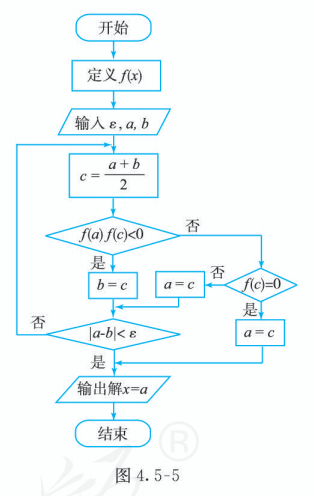
由例 2 可见, 用二分法求方程的近似解, 计算量较大,而且是重复相同的步骤. 因此,可以通过设计一定的计算程序, 借助信息技术完成计算. 图 4.5-5 就是表示二分法求方程近似解过程的程序框图. 有兴趣的同学, 可以在此基础上用有关算法语言编写程序, 利用信息技术求方程的近似解.
练习
1.
借助信息技术, 用二分法求函数 在区间 内零点的近似值 (精确度为 ).
2.
借助信息技术, 用二分法求方程 在区间 内的近似解(精确度为 ).
阅读与思考
中外历史上的方程求解
在人类用智慧架设的无数座从已知通向未知的金桥中,方程的求解是其中璀璨的一座. 虽然今天我们可以从教科书中了解各式各样方程的解法, 但这一切却经历了相当漫长的岁月.
我国古代数学家已比较系统地解决了某些类型方程求解的问题. 约公元 年编成的《九章算术》, 已经记载有开平方、开立方的开方方法, 这些开方问题与求解两项方程, 如求解 正根的方法是一致的; 7 世纪, 隋唐数学家王孝通找出了求三次方程正根的数值解法; 11 世纪, 北宋数学家贾宪在《黄帝九章算法细草》中提出的 “开方作法本源图”, 以“立成释锁法” 来解三次或三次以上的高次方程. 同时, 他还提出了一种更简便的 “增乘开方法”; 13 世纪, 南宋数学家秦九韶在《数书九章》中提出了 “正负开方术”, 提供了一种用算筹布列解任意数字方程的有效算法, 此法可以求出任意次代数方程的正根.
国外数学家对方程求解也有很多研究. 9 世纪, 阿拉伯数学家花拉子米 (Al-Khowarizmi, 约 780-850) 给出了一次方程和二次方程的一般解法; 1541 年,意大利数学家塔尔塔利亚 (N. Tartaglia, 约 1499-1557) 给出了三次方程的一般解法; 1545 年, 意大利数学家卡尔达诺 (G. Cardano, 1501-1576) 的名著《大术》一书中, 把塔尔塔利亚的解法加以发展, 并记载了费拉里 (L. Ferrari, 1522-1565)的四次方程的一般解法.
数学史上, 人们曾希望得到一般的五次及以上代数方程的根式解, 但经过长期的努力仍无结果. 1778 年, 法国数学大师拉格朗日 (J.-L. Lagrange, 1736-1813)提出了五次方程不存在根式解的猜想. 1824 年, 挪威年轻数学家阿贝尔 (N. H. Abel, 1802-1829) 成功地证明了五次及以上一般方程没有根式解. 1828 年, 法国天才数学家伽罗瓦 (E. Galois, 1811-1832) 巧妙而简洁地证明了存在不能用开方运算求解的具体方程, 同时还给出了一个代数方程能用根式求解的充要条件, 他完全解决了高次方程的求解问题, 并创立了对代数学发展影响深远的 “伽罗瓦理论”.
虽然指数方程、对数方程等超越方程和五次及以上的高次代数方程不能用代数运算求解, 但其数值解法却随着现代计算技术的发展得到了广泛的运用, 如本章介绍的二分法, 就是一种常见的利用计算技术的数值解法. 除了二分法, 牛顿法、拟牛顿法、弦截法等也都是典型的数值解法. 关于这些方法, 感兴趣的同学还可以查阅相关资料作进一步的了解.
4.5.3 函数模型的应用
我们知道, 函数是描述客观世界变化规律的数学模型, 不同的变化规律需要用不同的函数模型来刻画. 面临一个实际问题, 该如何选择恰当的函数模型来刻画它呢?
例 3
人口问题是当今世界各国普遍关注的问题. 认识人口数量的变化规律, 可以为制定一系列相关政策提供依据. 早在 1798 年, 英国经济学家马尔萨斯(T. R. Malthus, 1766-1834)就提出了自然状态下的人口增长模型
其中 表示经过的时间, 表示 时的人口数, 表示人口的增长率.
(1) 根据国家统计局网站公布的数据,我国 1950 年末、1959 年末的人口总数分别为 55196 万和 67207 万. 根据这些数据, 用马尔萨斯人口增长模型建立我国在 1950~1959 年期间的具体人口增长模型.
(2) 利用 (1) 中的模型计算 1951~1958 年各年末的人口总数. 查阅国家统计局网站公布的我国在 1951~1958 年间各年末的实际人口总数, 检验所得模型与实际人口数据是否相符.
(3) 以 (1) 中的模型作预测, 大约在什么时候我国人口总数达到 13 亿?
思考
尽管对马尔萨斯人口理论存在一些争议, 但它对人口学和经济学的发展都产生了一定的影响. 上网了解, 还有哪些人口模型, 它们与我们所学的函数有怎样的关系?
分析:
用马尔萨斯人口增长模型建立具体人口增长模型, 就是要确定其中的初始量 和增长率 .
解:
(1) 由题意知 , 设 1950~1959 年期间我国人口的年平均增长率为 ,根据马尔萨斯人口增长模型, 有
由计算工具得
因此我国在 年期间的人口增长模型为
(2) 分别取 , 由 可得我国在 年间的各年末人口总数; 查阅国家统计局网站, 得到我国 1951~1958 年各年末的实际人口总数,如表 4.5-4 所示.

根据 年我国人口总数的实际数据画出散点图, 并画出函数 的图象 (图 4.5-6).
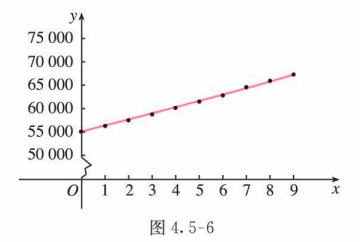
由表 4.5-4 和图 4.5-6 可以看出, 所得模型与 1950~1959 年的实际人口数据基本吻合.
(3) 将 代入
由计算工具得
所以, 如果人口按照 (1) 中的模型增长, 那么大约在 1950 年后的第 40 年(即 1990 年), 我国的人口就已达到 13 亿.
思考
事实上, 我国 1990 年的人口数为 11.43 亿, 直到 2005 年才突破 13 亿. 对由函数模型所得的结果与实际情况不符, 你有何看法?
解
因为人口基数较大, 人口增长过快, 与我国经济发展水平产生了较大矛盾, 所以我国从 20 世纪 70 年代逐步实施了计划生育政策. 因此这一阶段的人口增长条件并不符合马尔萨斯人口增长模型的条件, 自然就出现了依模型得到的结果与实际不符的情况.
在用已知的函数模型刻画实际问题时, 应注意模型的适用条件.
下面来解决章引言中的问题.
例 4
2010 年, 考古学家对良渚古城水利系统中一条水坝的建筑材料(草裏泥)上提取的草茎遗存进行碳 14 年代学检测, 检测出碳 14 的残留量约为初始量的 , 能否以此推断此水坝大概是什么年代建成的?
分析:
因为死亡生物机体内碳 14 的初始量按确定的衰减率衰减, 属于指数衰减, 所以应选择函数 , 且 , 且 建立数学模型.
解:
设样本中碳 14 的初始量为 , 衰减率为 , 经过 年后, 残余量为 y. 根据问题的实际意义, 可选择如下模型:
由碳 14 的半衰期为 5730 年, 得
于是
所以
由样本中碳 14 的残余量约为初始量的 可知,
即
解得
由计算工具得
因为 2010 年之前的 4912 年是公元前 2903 年, 所以推断此水坝大概是公元前 2903 年建成的.
练习
1.
已知 1650 年世界人口为 5 亿, 当时人口的年增长率为 ; 1970 年世界人口为 36 亿, 当时人口的年增长率为 .
(1) 用马尔萨斯人口模型计算, 什么时候世界人口是 1650 年的 2 倍? 什么时候世界人口是 1970 年的 2 倍?
(2) 实际上, 1850 年以前世界人口就超过了 10 亿; 而 2004 年世界人口还没有达到 72 亿. 你对同样的模型得出的两个结果有何看法?
2.
在一段时间内, 某地的野兔快速繁殖, 野兔总只数的倍增期为 21 个月, 那么 1 万只野兔增长到 1 亿只野兔大约需要多少年?
3.
1959 年, 考古学家在河南洛阳偃师市区二里头村发掘出了一批古建筑群, 从其中的某样本中检测出碳 14 的残余量约为初始量的 , 能否以此推断二里头遗址大概是什么年代的?
在实际问题中, 有的能应用已知的函数模型解决, 有的需要根据问题的条件建立函数模型加以解决.
例 5
假设你有一笔资金用于投资, 现有三种投资方案供你选择, 这三种方案的回报如下:
方案一: 每天回报 40 元;
方案二: 第一天回报 10 元, 以后每天比前一天多回报 10 元;
方案三: 第一天回报 0.4 元, 以后每天的回报比前一天翻一番.
请问,你会选择哪种投资方案?
分析:
我们可以先建立三种投资方案所对应的函数模型, 再通过比较它们的增长情况, 为选择投资方案提供依据.
解:
设第 天所得回报是 元, 则方案一可以用函数 进行描述; 方案二可以用函数 进行描述; 方案三可以用函数 进行描述. 三个模型中, 第一个是常数函数, 后两个都是增函数. 要对三个方案作出选择, 就要对它们的增长情况进行分析.
我们先用信息技术计算一下三种方案所得回报的增长情况 (表 4.5-5).
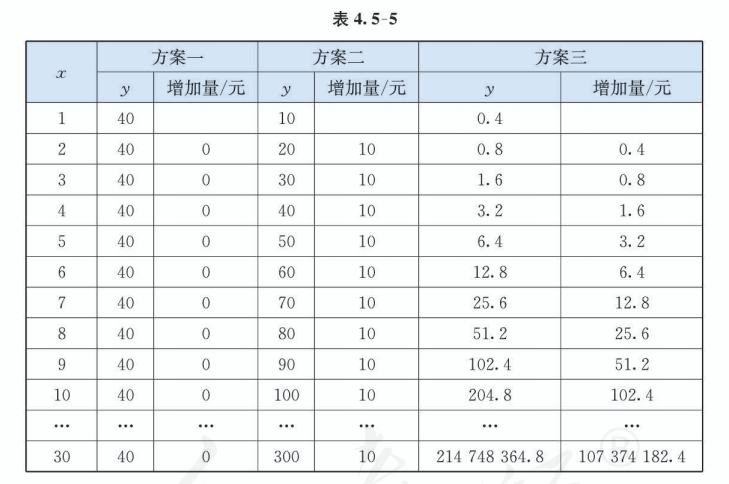
再画出三个函数的图象 (图 4.5-7).
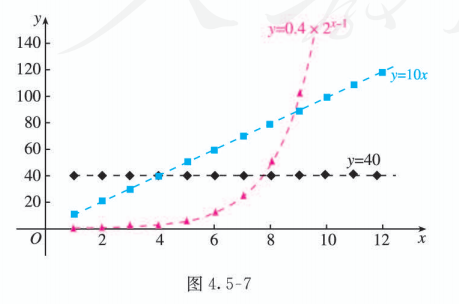
函数图象是分析问题的好帮手. 为了便于观察,用虚线连接离散的点.
解(续)
由表 4.5-5 和图 4.5-7 可知, 方案一的函数是常数函数, 方案二、方案三的函数都是增函数, 但方案三的函数与方案二的函数的增长情况很不相同. 可以看到, 尽管方案一、方案二在第 1 天所得回报分别是方案三的 100 倍和 25 倍, 但它们的增长量固定不变, 而方案三是 “指数增长”,其 “增长量” 是成倍增加的, 从第 7 天开始, 方案三比其他两个方案增长得快得多, 这种增长速度是方案一、方案二所无法企及的. 从每天所得回报看, 在第 天, 方案一最多; 在第 4 天, 方案一和方案二一样多, 方案三最少; 在第 天, 方案二最多; 第 9 天开始, 方案三比其他两个方案所得回报多得多, 到第 30 天, 所得回报已超过 2 亿元.
思考
根据这里的分析, 是否应作这样的选择: 投资 5 天以下选方案一,投资 天选方案二,投资 8 天以上选方案三?
解(续)
下面再看累计的回报数. 通过信息技术列表如下(表 4.5-6).
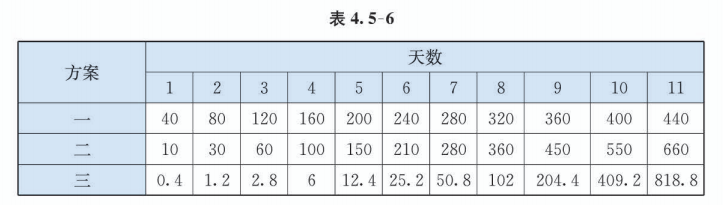
因此, 投资 天, 应选择方案一; 投资 7 天,应选择方案一或方案二; 投资 天,应选择方案二; 投资 11 天(含 11 天)以上,则应选择方案三.
上述例子只是一种假想情况, 但从中可以看到, 不同的函数增长模型, 增长变化存在很大差异.
例 6
某公司为了实现 1000 万元利润的目标, 准备制定一个激励销售人员的奖励方案: 在销售利润达到 10 万元时, 按销售利润进行奖励, 且奖金 (单位: 万元) 随销售利润 (单位: 万元) 的增加而增加, 但奖金总数不超过 5 万元, 同时奖金不超过利润的 . 现有三个奖励模型: , 其中哪个模型能符合公司的要求?
分析:
本例提供了三个不同增长方式的奖励模型, 按要求选择其中一个函数作为刻画奖金总数与销售利润的关系. 由于公司总的利润目标为 1000 万元,所以销售人员的销售利润一般不会超过公司总的利润. 于是, 只需在区间 上, 寻找并验证所选函数是否满足两条要求:第一,奖金总数不超过 5 万元,即最大值不大于 5 ; 第二, 奖金不超过利润的 , 即 .
不妨先画出函数图象, 通过观察函数图象, 得到初步的结论, 再通过具体计算, 确认结果.
解:
借助信息技术画出函数 的图象(图 4.5-8). 观察图象发现, 在区间 上, 模型 的图象都有一部分在直线 的上方, 只有模型 的图象始终在 的下方, 这说明只有按模型 进行奖励时才符合公司的要求.
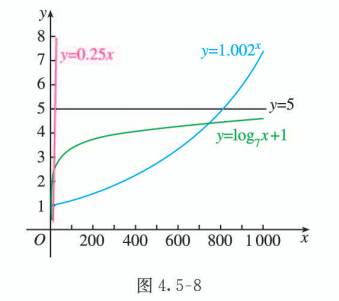
下面通过计算确认上述判断.
先计算哪个模型的奖金总数不超过 5 万元.
对于模型 , 它在区间 上单调递增, 而且当 时, ,因此, 当 时, , 所以该模型不符合要求;
对于模型 , 由函数图象, 并利用信息技术, 可知在区间 内有一个点 满足 , 由于它在区间 上单调递增, 因此当 时, ,所以该模型也不符合要求;
对于模型 , 它在区间 上单调递增, 而且当 时, , 所以它符合奖金总数不超过 5 万元的要求.
再计算按模型 奖励时, 奖金是否不超过利润的 , 即当 时, 是否有 , 即 成立.
令 , 利用信息技术画出它的图象(图 4.5-9).
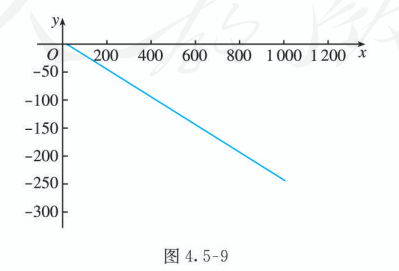
由图象可知函数 在区间 上单调递减, 因此
即
所以, 当 时, , 说明按模型 奖励, 奖金不会超过利润的 .
综上所述, 模型 确实能符合公司要求.
归纳
用函数建立数学模型解决实际问题的基本过程如下:
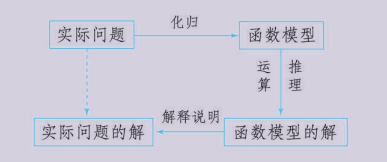
这一过程包括分析和理解实际问题的增长情况 (是 “对数增长” “直线上升” 还是 “指数爆炸”) ; 根据增长情况选择函数类型构建数学模型, 将实际问题化归为数学问题; 通过运算、推理求解函数模型; 用得到的函数模型描述实际问题的变化规律, 解决有关问题. 在这一过程中, 往往需要利用信息技术帮助画图、运算等.
练习
1.
某地今年 1 月, 2 月, 3 月患某种传染病的人数分别为 . 为了预测以后各月的患病人数,甲选择了模型 , 乙选择了模型 , 其中 为患病人数, 为月份数, , 都是常数. 结果 4 月, 5 月, 6 月份的患病人数分别为 , 你认为谁选择的模型更符合实际?
2.
由于提高了养殖技术并扩大了养殖规模, 某地的肉鸡产量在不断增加. 年的 11 年, 上市的肉鸡数量如下:

同期该地的人口数如下:

(1) 分别求出能近似地反映上述两组数据变化规律的函数;
(2) 如果 2017 年该地上市的肉鸡基本能满足本地的需求,那么 2018 年是否能满足市场的需求?
(3) 按上述两表的变化趋势, 你对该地 2018 年后肉鸡市场的发展有何建议?
习题 4.5
复习巩固
1.
下列函数图象与 轴均有交点, 其中不能用二分法求其零点的是 _ _ _ . (填写上所有符合条件的图号)
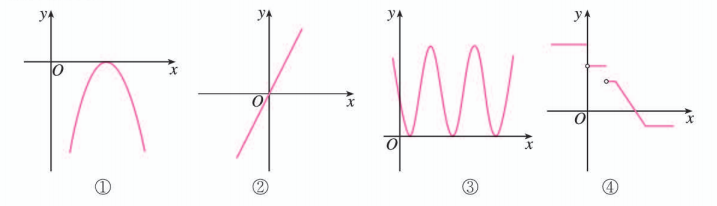
2.
已知函数 的图象是一条连续不断的曲线, 且有如下对应值表:

函数 在哪几个区间内一定有零点? 为什么?
3.
已知函数 , 求证: 方程 在 内至少有两个实数解.
4.
利用信息技术, 用二分法求函数 的零点 (精确度为 0.1 ).
5.
利用信息技术, 用二分法求方程 的近似解 (精确度为 0.1 ).
6.
一种专门占据内存的计算机病毒, 开机时占据内存 , 然后每 3 分自身复制一次, 复制后所占内存是原来的 2 倍. 那么开机后多少分, 该病毒会占据 内存 ?
综合运用
7.
设函数 , 且 , 求证: 函数 在 内至少有一个零点.
8.
已知函数 ,
(1) 求函数 的解析式;
(2) 利用信息技术, 画出函数 的图象;
(3) 求函数 的零点(精确度为 0.1 ).
9.
如图, 某池塘里浮萍的面积 (单位: ) 与时间 (单位: 月) 的关系为 . 关于下列说法:
(1) 浮萍每月的增长率为 1 ;
(2) 第 5 个月时, 浮萍面积就会超过 ;
(3) 浮萍每月增加的面积都相等;
(4) 若浮萍蔓延到 所经过的时间分别是 , 则 .
其中正确的说法是 ( ).
(A) (1)(2)
(B) (1)(2)(3)
© (1)(2)(4)
(D) (1)(2)(3)(4)

10.
一种药在病人血液中的量保持在 以上时才有疗效, 而低于 时病人就有危险.现给某病人的静脉注射了这种药 , 如果药在血液中以每小时 的比例衰减, 那么应在什么时间范围再向病人的血液补充这种药(精确到 )?
11.
人类已进人大数据时代. 目前, 数据量已经从 级别跃升到 ( 乃至 级别. 曾经的研究结果表明, 年全球产生的数据量为 , 年的数据量为 年增长到 , 年的数据量更是高达 .
(1) 为了较好地描述 2008 年起全球产生的数据量与时间 (单位: 年)的关系, 根据上述数据信息, 从函数 和 中选择一个, 并求出解析式.
(2) 根据(1)中所求函数模型, 估计 2018 年全球所产生的数据量, 并与所公布数据比较,你有何看法?
12.
某地不同身高的未成年男性的体重平均值如下表:

(1) 根据表中提供的数据建立恰当的函数模型, 使它能近似地反映这个地区未成年男性平均体重 (单位: )与身高 (单位: ) 的函数关系, 并写出这个函数的解析式.
(2) 若体重超过相同身高男性体重平均值的 1.2 倍为偏胖, 低于 0.8 倍为偏瘦, 那么该地一名身高为 , 体重为 的在校男生的体重是否正常?
拓广探索
13.
有一道题 “若函数 在区间 内恰有一个零点, 求实数 的取值范围”, 某同学给出了如下解答:
由 , 解得 .
所以, 实数 的取值范围是 .
上述解答正确吗? 若不正确, 请说明理由, 并给出正确的解答.
14.
从甲地到乙地的距离约为 , 经多次实验得到一辆汽车每小时耗油量 (单位: L)与速度 (单位: 的下列数据:

为了描述汽车每小时耗油量与速度的关系, 现有以下三种模型供选择:
(1) 选出你认为最符合实际的函数模型, 并写出相应的函数解析式;
(2) 从甲地到乙地, 这辆车应以什么速度行驶才能使总耗油量最少?
文献阅读与数学写作
选学内容, 不作为考试要求.
对数概念的形成与发展
对数的发明、解析几何的创始和微积分的建立被恩格斯并称为 17 世纪数学的三大成就. 对数的发明及其计算是数学史上的重大事件, 天文学界更是以近乎狂喜的心情来迎接这一发明. 意大利科学家伽利略 (Galileo Galilei, 1564-1642)说: “给我空间、时间及对数, 我就可以创造一个宇宙.” 法国数学家拉普拉斯 (P._S. Laplace, 1749-1827) 也曾评价道: “因为省时省力, 对数倍增了天文学家的寿命.”
作为重要而简便的计算工具, 对数是如何产生和发展的? 在数学的发展、人类社会的发展历史中起了什么作用? 请你按以下要求, 查阅与对数有关的文献,自己选题, 写一篇数学小论文.
一、主题
- 对数概念形成和发展的过程.
- 对数对简化运算的作用.
二、实施建议
- 选题: 根据个人兴趣, 围绕主题, 初步确定选题范围.
- 分组: 将相近选题的 人分为一个小组, 确定一名组长.
- 分配任务: 根据个人的具体情况, 经小组共同商议, 由组长确定每人的具体任务.
- 搜集资料: 针对具体的论文题目, 通过互联网、书店、图书馆等多种途径搜集素材, 包括文字、图片、数据以及音像资料, 并记录相关资料.
- 素材整理: 用论文的形式展现小组的实践成果.
- 交流讨论: 开展组内或全班的交流、讨论和总结.
三、参考选题
- 对数产生的背景.
- 对数发明的过程.
- 对数的具体应用.
- 对数对简化运算的作用.
- 对数对人类文明进步的贡献.