2.3 二次函数与一元二次方程、不等式
2024-01-21 22:55:59 新建
在初中, 我们从一次函数的角度看一元一次方程、一元一次不等式, 发现了三者之间的内在联系, 利用这种联系可以更好地解决相关问题. 对于二次函数、一元二次方程和一元二次不等式, 是否也有这样的联系呢? 先来看一个问题.
问题
园艺师打算在绿地上用栅栏围一个矩形区域种植花卉. 若栅栏的长度是 , 围成的矩形区域的面积要大于 , 则这个矩形的边长为多少米?
解 第1部分
设这个矩形的一条边长为 , 则另一条边长为 . 由题意, 得
其中 . 整理得
求得不等式(1)的解集, 就得到了问题的答案.
定义
一般地, 我们把只含有一个未知数, 并且未知数的最高次数是 2 的不等式, 称为一元二次不等式 (quadratic inequality with one unknown). 一元二次不等式的一般形式是
其中 均为常数, .
思考
在初中, 我们学习了从一次函数的观点看一元一次方程、一元一次不等式的思想方法. 类似地, 能否从二次函数的观点看一元二次不等式, 进而得到一元二次不等式的求解方法呢?
解 第2部分
下面, 我们先考察一元二次不等式 与二次函数 之间的关系.
分析1
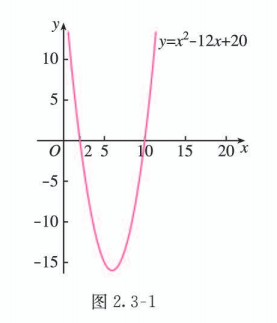
如图 2.3-1, 在平面直角坐标系中画出二次函数 的图象, 图象与 轴有两个交点. 这两个交点的横坐标就是方程 的两个实数根 , , 因此二次函数 的图象与 轴的两个交点是 和 .
定义
一般地, 对于二次函数 , 我们把使 的实数 叫做二次函数 的零点.
分析2
于是, 二次函数 的两个零点是 .
分析3
从图 2.3-1 可以看出, 二次函数 的两个零点 将 轴分成三段. 相应地, 当 或 时, 函数图象位于 轴上方, 此时 , 即 ; 当 时, 函数图象位于 轴下方, 此时 , 即 . 所以, 一元二次不等式 的解集是
解 第3部分
因为 , 因此当围成的矩形的一条边长 满足 时, 围成的矩形区域的面积大于 .
上述方法可以推广到求一般的一元二次不等式 和 的解集. 因为一元二次方程的根是相应一元二次函数的零点, 所以先求出一元二次方程的根, 再根据二次函数图象与 轴的相关位置确定一元二次不等式的解集.
我们知道, 对于一元二次方程 , 设 , 它的根按照 可分为三种情况. 相应地, 二次函数 的图象与 轴的位置关系也分为三种情况. 因此, 我们分三种情况来讨论对应的一元二次不等式 和 的解集 (表 2.3-1).
表 2.3-1 二次函数与一元二次方程、不等式的解的对应关系
| 的图象 | 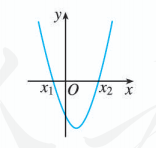 |
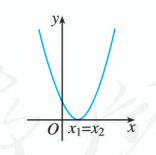 |
 |
| 的根 | 有两个不相等的实数根 | 有两个相等的实数根 | 没有实数根 |
| 的解集 | , 或 | ||
| 的解集 |
例 1
求不等式 的解集.
分析:
因为方程 的根是函数 的零点, 所以先求出 的根, 再根据函数图象得到 的解集.
解:
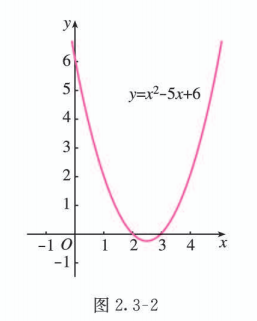
对于方程 , 因为 , 所以它有两个实数根. 解得 .
画出二次函数 的图象 (图 2.3-2), 结合图象得不等式 的解集为 , 或 .
例 2
求不等式 的解集.
解:
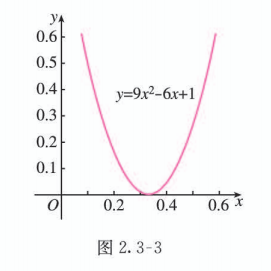
对于方程 , 因为 , 所以它有两个相等的实数根, 解得 .
画出二次函数 的图象(图 2.3-3), 结合图象得不等式 的解集为 .
对于二次项系数是负数(即 )的不等式,可以先把二次项系数化成正数, 再求解.
例 3
求不等式 的解集.
解:
不等式可化为 .
因为 , 所以方程 无实数根.
画出二次函数 的图象 (图 2.3-4).
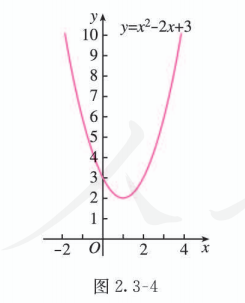
结合图象得不等式 的解集为 .
因此, 原不等式的解集为 .
思考
现在, 你能解决第 2.1 节的 “问题 2 ” 了吗?
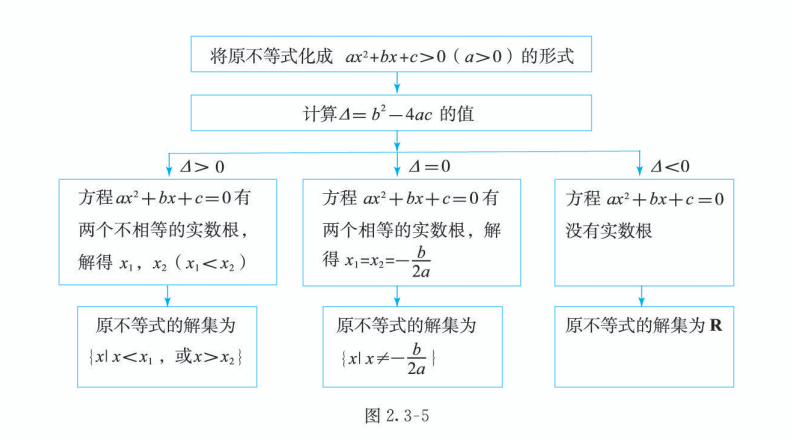
利用框图可以清晰地表示求解一元二次不等式的过程. 这里, 我们以求解可化成 形式的不等式为例, 用框图表示其求解过程(图 2.3-5).
练习
1.
求下列不等式的解集:
(1) ;
(2) ;
(3) ;
(4) ;
(5) ;
(6) .
2.
当自变量 在什么范围取值时,下列函数的值等于 0 ? 大于 0 ? 小于 0 ?
(1) ;
(2) ;
(3) ;
(4) .
利用一元二次不等式可以解决一些实际问题, 下面看两个例子.
例 4
一家车辆制造厂引进了一条摩托车整车装配流水线, 这条流水线生产的摩托车数量 (单位: 辆)与创造的价值 (单位: 元)之间有如下的关系:
若这家工厂希望在一个星期内利用这条流水线创收 60000 元以上, 则在一个星期内大约应该生产多少辆摩托车?
解:
设这家工厂在一个星期内大约应该利用这条流水线生产 辆摩托车, 根据题意, 得
移项整理, 得
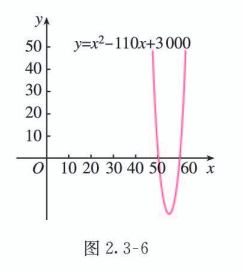
对于方程 , 方程有两个实数根 .
画出二次函数 的图象 (图 2.3-6), 结合图象得不等式 的解集为 ,从而原不等式的解集为
因为 只能取整数值, 所以当这条流水线在一周内生产的摩托车数量在 辆时, 这家工厂能够获得 60000 元以上的收益.
例 5
某种汽车在水泥路面上的刹车距离 (单位: ) 和汽车刹车前的车速 (单位: ) 之间有如下关系:
在一次交通事故中, 测得这种车的刹车距离大于 ,那么这辆汽车刹车前的车速至少为多少 (精确到 )?
刹车距离是指汽车刹车后由于惯性往前滑行的距离.
解:
根据题意, 得
移项整理, 得
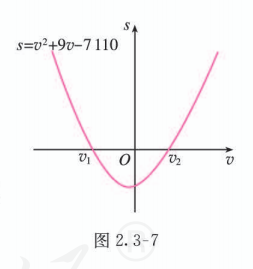
对于方程 , 方程有两个实数根
画出二次函数 的图象(图 2.3-7),结合图象得不等式的解集为 , 或 , 从而原不等式的解集为
因为车速 , 所以 . 而 , 所以这辆汽车刹车前的车速至少为 .
类似地, 第 2.1 节的不等式(1)经移项整理, 得 . 用上述方法解这个不等式, 得 . 所以, 当每本杂志的定价不低于 2.5 元且不超过 4 元时,提价后的销售总收人不低于 20 万元.
练习
1.
是什么实数时, 有意义?
2.
如图, 在长为 , 宽为 的矩形地面的四周种植花卉, 中间种植草坪. 如果要求花卉带的宽度相同, 且草坪的面积不超过总面积的一半, 那么花卉带的宽度应为多少米?

3.
某网店销售一批新款削笔器, 每个削笔器的最低售价为 15 元. 若按最低售价销售, 每天能卖出 30 个; 若一个削笔器的售价每提高 1 元, 日销售量将减少 2 个. 为了使这批削笔器每天获得 400 元以上的销售收人, 应怎样制定这批削笔器的销售价格?
习题 2.3
复习巩固
1.
求下列不等式的解集:
(1) ;
(2) ;
(3) ;
(4) .
2.
是什么实数时, 下列各式有意义?
(1) ;
(2) .
综合运用
3.
已知 , 求 .
4.
一名同学以初速度 坚直上抛一排球, 排球能够在抛出点 以上的位置最多停留多长时间 (精确到 )?
若不计空气阻力, 则坚直上拋的物体距离拋出点的高度 与时间 满足关系 , 其中 .
5.
已知集合 ,求 .
拓广探索
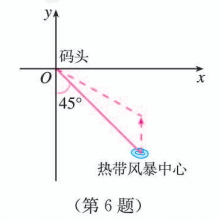
6.
如图, 据气象部门预报, 在距离某码头南偏东 方向 处的热带风暴中心正以 的速度向正北方向移动, 距风暴中心 以内的地区都将受到影响. 据以上预报估计, 从现在起多长时间后, 该码头将受到热带风暴的影响, 影响时间大约为多长 (精确到0.1 h)?